math notation can be much better
Math notation. It’s not great. Let’s make it less not great.
Math Needs Dialects
In Surely Your Joking, Richard Feynman came up with his own notation for trigonometric functions (sin, cos, etc.) which he felt was better than the usual notation, but ended up abandoning it: When he tried to show other people his work, no one understood it. Universality is the main benefit of a common, if flawed, math notation.
But math notation is used both for (1) communication and (2) for performing computations and wrestling with ideas. If better notation can help you with (2), it is worth separating these two uses. The current universal language of math is maintained for (1), and people can have their own dialects for (2).
Math is the user interface for logical truth. We’ve spent hundreds of thousands or more in man hours optimizing the smartphone UI, we must demand no less for math.
Of course people will have their opinions about which notation is better. Ideally, there will be libraries distributed online for different collections of math notation, perhaps as LaTeX packages, just as there are different and opinionated programming languages and frameworks. Math papers will “import” from these libraries at the beginning and provide readers with a link to documentation.
In this post we’ll be talking about a variety of improvements to math notation.
Prefix Notation
Which one is more readable? Infix notation: \[2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29,\] or prefix notation: \[+(2, 3,5,7,11,13,17,19,23,29)?\]
Infix operations are fine for a few numbers, but it is a pain for large amounts of numbers. You have to look at a bunch of plus signs, and make sure there’s no sneaky minus or division signs in there.
Summation and product notation allow for prefix notation, but you have to rewrite your expressions in terms of an index variable or index set. We should be able to simply express an operation applied over a list (much like reduce of map, filter, and reduce). Prefix notation let’s us do this easily.
Going Beyond Left to Right
Written math is done on paper and whiteboards, which are open and free, yet, with very few exceptions, we restrict our notation to be a series of symbols written neatly from left to right. Today’s screens are equally boundless. We must go beyond the narrow left to right mentality.
Lists are usually written horizontally. \[(2, 3,5,7,11).\]
We could try vector-style vertical notation. The line breaks enhance legibility. We can distinguish these from vectors by noting that lists use commas.
\[ \begin{pmatrix} 2,\\3, \\ 5, \\7,\\11 \end{pmatrix}. \]
However, with many operands, this takes up quite a lot of vertical space. Let’s allow any arrangement of the list entries. The order is determined always by going left to right, top to bottom.
\[\left(\begin{array}{ccc} 2,3,\\ 5,7,11 \end{array}\right)\]
To make sure these are not confused with matrices, we can fully enclose them in a box or circle:
\[\boxed{\begin{array}{ccc} 2,3,\\ 5,7,11 \end{array}}\]
This can make function composition look nicer.
\(f(g(h(x), h(y)))\)
becomes
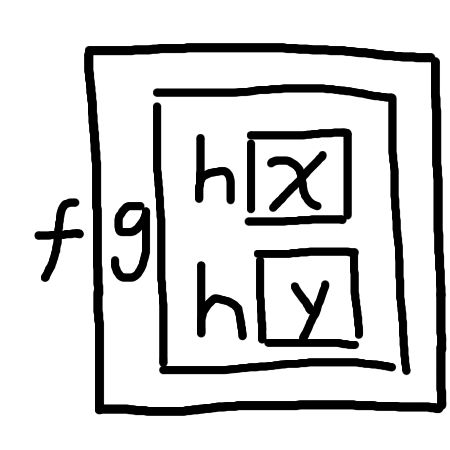
Much better. Maybe if we decide to use this notation for function arguments, we can consider explictly writing out function application. Sometimes this represented with a dollar sign like in Haskell. I think we can do better, here’s some ideas:
\[f \leftarrow \boxed{x}\] \[f \lhd \boxed{x}\] \[f \dashv \boxed{x}\]
There are a huge amount of LaTeX arrows, why let them go unused?
While we’re at it, we might as well have a notation for map (applying \(f\) to each element of a list):
\(f \leftleftarrows \boxed{x, y, z} = (f(x), f(y), f(z))\)
Circles
Next, I think we can make math evoke more reverence. Many religions, spiritual practices, and cults have cool diagrams and symbols. If math looked cooler, perhaps we would have more mathematicians. Certainly, we would have much better cults like the Church of Turing, the Galois Group, and the Terrence Taoists. They would have awesome rituals, like forgoing grant money to work on the Goldbach Conjecture. Secrets would be shared with Shamir’s secret sharing scheme. And the doorway to their Temple’s secret chamber would be guarded by one guard who always tells the truth, one guard who always lies, and one guard with a very sharp compass.
One way to making math more reverent is circles and regular polygons. Euclidean geometry has ton of this. (Unfortunately most math today is done with algebra. I hope one day we return to doing number theory with lines and points.)
For example, polynomials are usually written like \(x^3+x^2+x+1\). With prefix notation it looks a bit better, as \(+(x^3, x^2, x, 1)\). But let’s apply the principle of Going Beyond Left to Right, and add circles and regular polygons!
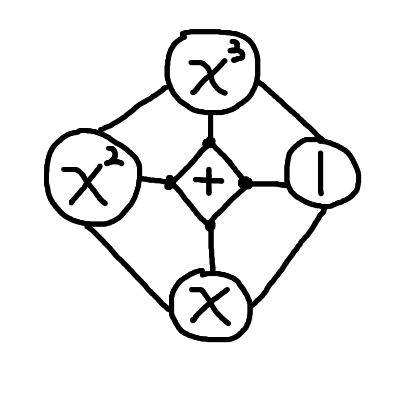
This doesn’t just look cooler. It also gives you more information at a glance. The top entry is the term of highest degree. When terms of certain degrees are missing, you will see blank circles in their place (whereas with regular notation, you have to read through the whole thing carefully).
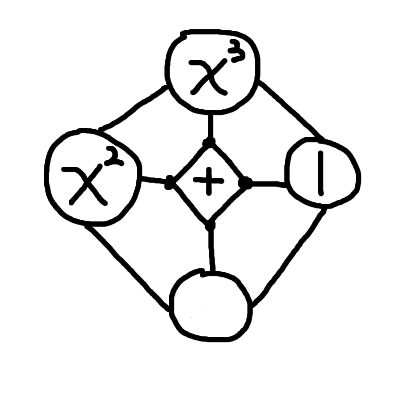
To be clear, we don’t need to use this in our everyday math. In writing, we have calligraphy for important decorations, very readable printed text for documents, and chicken scratch for everyday use. We can also separate math notation into a fancy version used for presentations and movies, a readable version used for papers and textbooks, and a messy version for getting things done.
Syntax Highlighting
Code is syntax highlighted. Math can be too.
For math, this can apply both for text and formulas. For text, we can give different colors to variables, math terminology, descriptors, etc.
Compare this:

To this:

With regular text, it’s all the same font color, and you have to read through it to figure out where the main points. With color, the structure of text becomes easy to discern at a glance. Moreover, color can also be used to demonstrate parts that are the same, so you don’t have to keep looking back and forth to compare them.
We can also add color to formulas and equations.
\[ \left(\left\lfloor \frac{y}{12}\right\rfloor + y \text{ mod } 12 + \left\lfloor \frac{y \text{ mod }12}{4}\right\rfloor\right) \text{ mod }7 + \text{anchor} = \text{Doomsday} \]
A basic usage is adding colors to brackets, so it’s easy to see which ones match.
\[ \require{color} % make sure the color extension is active {\color{red}{% \Bigl( {\color{blue}{% \Bigl( {\color{green}{\left\lfloor \dfrac{y}{12} \right\rfloor}} +\, y \bmod 12 +\, {\color{green}{\left\lfloor \dfrac{\,y \bmod 12\,}{4} \right\rfloor}} \Bigr) }} \bmod 7 \Bigr) }} +\;\text{anchor} =\;\text{Doomsday} \]
But you can also give it the whole syntax highlighting treatment, giving color to variables, operations, constants, etc.
\[ \require{color} % pull in the color extension {\color{red}{% \Bigl( {\color{green}{% \left\lfloor {\color{blue}{\dfrac{\color{SkyBlue}{y}}{12}}} \right\rfloor }}\!+\! {\color{SkyBlue}{y}}\! {\color{blue}{\bmod}}\! 12\!+\! {\color{green}{% \left\lfloor {\color{blue}{\dfrac{\color{SkyBlue}{y}\;\bmod\;12}{4}}} \right\rfloor }} \Bigr) }}\! {\color{blue}{\bmod}}\! 7 +\; {\color{SkyBlue}{\text{anchor}}} =\; {\color{SkyBlue}{\text{Doomsday}}} \]
Of course, with current LaTeX, this is a nightmare, look at this:
\require{color}
{\color{red}{%
\Bigl(
{\color{green}{%
\left\lfloor
{\color{blue}{\dfrac{\color{SkyBlue}{y}}{12}}}
\right\rfloor
}}\!+\!
{\color{SkyBlue}{y}}\!
{\color{blue}{\bmod}}\! 12\!+\!
{\color{green}{%
\left\lfloor
{\color{blue}{\dfrac{\color{SkyBlue}{y}\;\bmod\;12}{4}}}
\right\rfloor
}}
\Bigr)
}}\!
{\color{blue}{\bmod}}\! 7
+\;
{\color{SkyBlue}{\text{anchor}}}
=\;
{\color{SkyBlue}{\text{Doomsday}}}
But I am sure with the power of Large Language Models, automatically adding colors according to user provided rules can become easy.
Ergonomic Symbols
The space of possible ways to represent common mathematical operations has not been sufficiently explored. Typically, we abberviate the name of an operation and use that as the notation (“sin”, “log”, etc.). This can look confusing because we also use Latin letters for variable names, and also looks a bit ugly.
For instance, here is Trigonometry 2.0, described by Richard Feynman and reimagined by Oliver Burt. 1
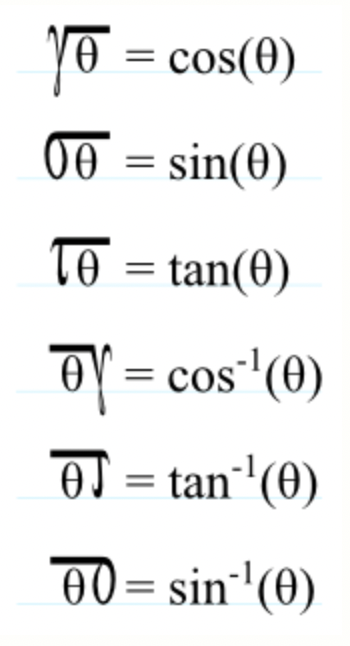
And possible symbols for infimum (top) and supremum (bottom) I came up with, that reflect the meanings of each:
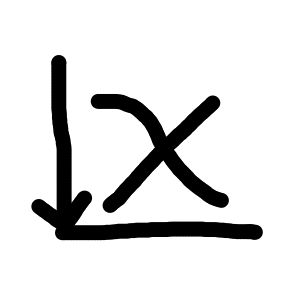

It is also worth exploring if alternate ways of representing things offer “affordances” that make it intutively obvious how to manipulate these expressions. For instance, the fraction symbol makes it clear that you can “cancel” common factors from the top and the bottom.
One example of such is the many proposals for an alternative logarithm notation. There is a cool 3Blue1Brown video describing one of these, which unifies logarithm, exponentiation, and roots.
I came up with one too (for \(\log_a b\)).
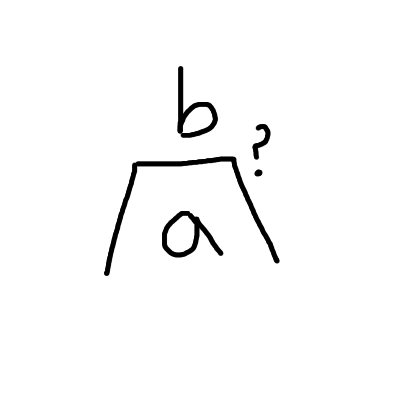
The question mark shows that this is saying, \(a^? = b\). This also offers an affordance of making it easy to see you can cancel between the base and argument of the two separate logarithms when they are the same.
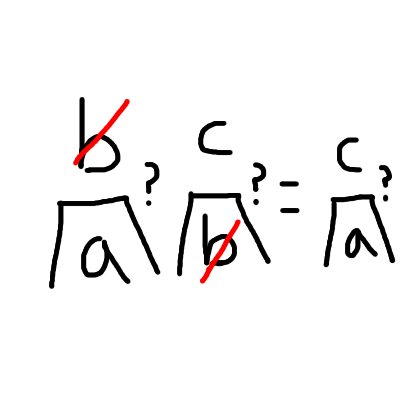
Of course, this also can be misleading, because if the base of the right logarithm was \(2b\) instead, you cannot simply cancel like this. As the saying goes, “The price of metaphor is eternal vigilance.”
Inline Annotations
The usual way of writing math is describing all your variables and operations in text, and then you use them within math expressions. The reader then has to look back and forth between these to figure out what’s going on.
Let’s annotate the symbols inline, to save the reader the effort.
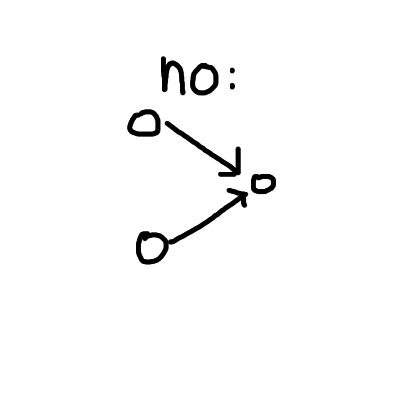
One example is that the sizes of all matrices and vectors should always be annotated.
Say no to this: \[A = U\Sigma V^T\]
And yes to this:
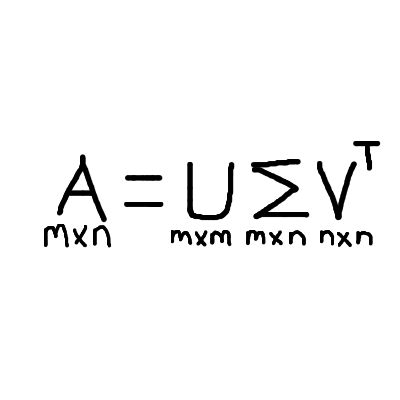
Even better, we can arrange the matrix column/row sizes to be more intuitively positioned:
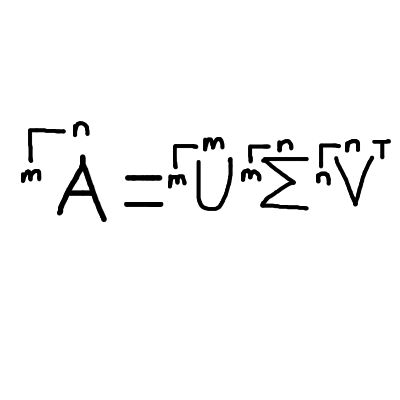
Furthermore, annotations can end up awkwardly positioned with left to right infix notation:
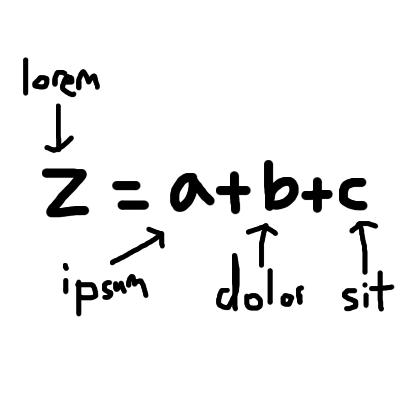
Using prefix notation and going beyond left to right, we can make this much clearer:
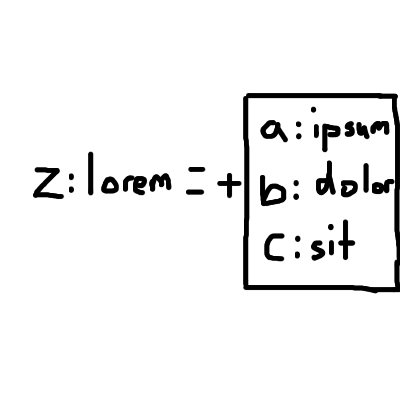
(Yes, it is looking a bit like JSON now.)
Annotations do take up more space. But today is not like Fermat’s time, where people competed in math golf to fit whole proofs in book margins 2. We have enough space. If it takes 10x more space to make a proof 2x more easy to understand, I think that’s a great trade.
Pictures over Words
Pictures are easier to understand than words. Especially math words, with are often derived from Latin.
For instance, injective and surjective. If you knew what these words meant, but forgot which was which, the prefixes “in” and “sur” are not very helpful unless you know what they mean.
But what about these pictures for injective (top) and surjective (bottom):
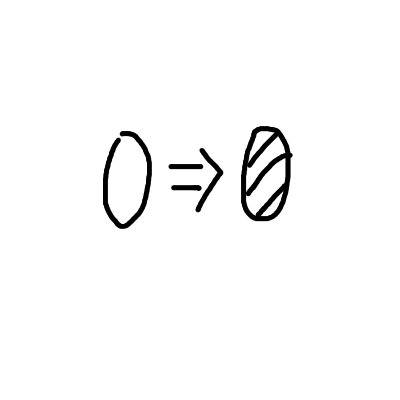
For injectivity, the top image shows how no two things in the domain can be mapped to the same thing in the codomain. For surjectivity, the bottom image shows how every element of the codomain is reachable from some element in the domain.
Now you can just draw this quick picture. No one is getting the meanings mixed up. The reading will change of course, because otherwise you still need to remember the names.
We could rename injective to “collisionless” and surjective to “covers everything”. These names are more obvious at a glance.
That leads us to a new topic: names of things in mathematics are not great, and can made much clearer. For instance, using people’s names for things is confusing because it doesn’t give any information about the thing itself. On the other hand, the “Four Color Theorem” is a name that is descriptive.
Some possible renamings:
Pythagorean Theorem: “Right Triangle Side-length Theorem”
Banach–Tarski Paradox: “Ball Duplication Paradox”
Stirling’s Approximation: “Good Factorial Approximation 1”
My favorite name is probably the Chicken McNugget Theorem of number theory.
Legibility Enhancements
Last but not least, the most important thing about math, especially when handwritten, is making it legible, otherwise you’ll be prone to confusion and silly mistakes. John Kerl has an excellent list of tips for making symbols unambiguous.
These are the ones I’ve used the most:
- Always make lowercase L cursive
- Put a hook on the bottom of t, to distinguish it from +
- Cross lowercase z, to distinguish it from 2.
- Make the top of 4 open, to distinguish it from 9
- Cross 7, to distinguish it from 1